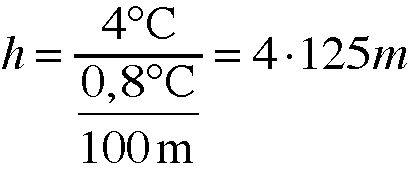Der trockenadiabatische Hebungsgradient |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Eine mathematisch-physikalische Betrachtung der Grundlagen adiabatischer Zustandsänderungen |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ja ich weiß, ein fürchterliches Wortungetüm! Und als ob das nicht schon reichen würde, gibt es dazu noch einen feuchtadiabatischen Hebungsgradienten und schließlich noch den Schichtungsgradienten. Wer jedoch in der Sportfliegerei ohne Motor hoch hinaus will (oder aber möglichst lange oben bleiben), der sollte mindestens eine Ahnung von diesen sperrigen Begriffen haben und ihre Zusammenhänge kennen. Doch erst mal, in aller gebotenen Kürze der Reihe nach: Schon jeder Fußgänger weiß, so er mal auf einen hohen Berg gekraxelt ist, dass es mit zunehmender Höhe kälter wird; auch Segel-, Drachen- und Gleitschirmflieger mummeln sch gut ein, wenn es etwas höher gehen soll. Die Ursache hierfür liegt auf der Hand: Die Sonnenstrahlen, die einzig und allein für den Energienachschub auf der Erde verantwortlich sind, durchdringen die Lufthülle ungehindert; das bedeutet, dass von der Energie, die sie transportieren (so gut wie) nichts an die Lufthülle abgegeben wird. Stellen wir uns dazu vor, wie an einem schönen Sommertag um die Mittagszeit die Sonne hoch am Himmel steht. Dieser gleißend helle Ball erscheint am Boden unseres Luftmeeres nicht anders, als wenn wir ihn aus einem Flugzeug in großer Höhe oder gar aus dem Weltraum außerhalb der Lufthülle betrachten. Wenn sich die elektromagnetische Strahlung der Sonne, also das sichtbare Licht, beim relativ kurzen Weg durch die Lufthülle nicht wesentlich verändert, dann kann unsere Atmosphäre diese Energiequelle nicht entscheidend "angezapft" haben! Wir klammern hier mal die Vorgänge in der Stratosphäre und in der Ionosphäre getrost aus, da wir Flieger uns in diesen Höhen eher selten aufhalten und dort oben, mangels Wasserdampf gar kein Wettergeschehen mehr stattfindet. Erst am Abend unseres Sommertages sehen wir eine Veränderung, wenn die Sonne als roter Ball untergeht. Jetzt ist der Weg der Sonnenstrahlen durch die Atmosphäre ungleich länger als am Mittag und außerdem wird durch den flachen Einfallswinkel der Sonnenstrahlen auf die Lufthülle ein Teil dieser Strahlen wie von einem Spiegel wieder in den Weltraum zurück reflektiert. Besonders das kurzwellige blaue Sonnenlicht verabschiedet sich auf diese Weise und der rote Strahlungsanteil wird demzufolge größer. Am Tag dringt das Sonnenlicht somit ungehindert durch die unsichtbare Lufthülle und erwärmt erst am Grund des Luftozeans den Erdboden, während die Luft selbst von den Sonnenstrahlen nicht erwärmt wird. Im Kleinen lässt sich dieses Phänomen auch bei Sonnemschein an jedem Fenster überprüfen: Während das durchsichtige Glas relativ kühl bleibt, haben sich an der Außenseite die Fensterrahmen je nach Farbe kräftig aufgeheizt. Der solchermaßen erwärmte Erdboden wirkt nun als Heizplatte und erwärmt die über ihm liegende Luft. Und je weiter wir uns von dieser Wärmequelle in größere Höhen wegbewegen, desto kälter wird es. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
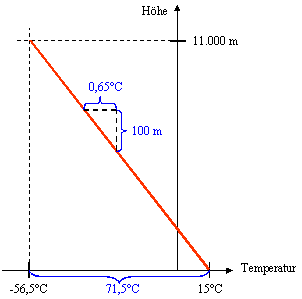
Der Schichtungsgradient
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Luftpakete im RucksackNehmen wir auf unserem Weg zur Zugspitze, egal ob zu Fuß, mit der Zahnradbahn oder in der bequemen Seilbahn in Gedanken einen gut eingepackten Kubikmeter Luft mit. Gut eingepackt soll heißen, dass wir eine Verpackung wählen, die das Luftpaket vollständig wärmeisoliert und somit keinerlei Wärme hinein oder herauslässt. Auf der anderen Seite soll diese Verpackung gewichtslos, beliebig flexibel und dehnbar sein, so dass unser Luftpaket immer das gerade benötigte Volumen zur Verfügung hat ohne zusammengedrückt oder auseinandergezogen zu werden. Diesen Zustand einer vollkommenen Wärmeisolierung nennt der Physiker adiabatisch, womit schon ein kleiner aber wesentlicher Teil des obigen Wortungetüms erklärt wäre. Auf dem Weg nach oben nimmt der äußere Luftdruck kontinuiertlich ab. Der Luftdruck wird erzeugt durch das Gewicht der über uns liegenden Luftmassen. Je höher wir steigen, um so weniger Luft liegt über uns und um so geringer wird damit der von ihr erzeugte Druck. Wir Menschen spüren solche allmählichen Luftdruckänderungen nur, wenn wir verschnupft sind und meist, wenn der Luftdruck beim Abstieg wieder zunimmt. Wir müssen dann häufig schlucken, damit der Druck aus den Ohren verschwindet. Die Luftdruckabnahme mit der Höhe kann mit Hilfe der internationalen Höhenformel berechnet werden:
1013,25hPa ist der Druck am Boden in Meereshöhe. Gibt man für h die gewünschte Höhe in km ein, so berechnet die Formel den Druck in eben dieser Höhe. Unser Luftpaket reagiert beim Aufstieg auf den nachlassenden äußeren Luftdruck: Es dehnt sich aus und wird größer. Luft die sich ausdehnt, wird aber kälter! Nach diesem Prinzip funktioniert unser Kühlschrank, außerdem haben wir den umgekehrten Effekt bestimmt schon mal beim Aufpumpen eines Reifens bemerkt, so wir dies von Hand mit einer Luftpumpe vorgenommen und keinen Kompressor verwendet haben. Die Luftpumpe wird warm! Natürlich wird auch der Kompressor warm, weshalb wir tunlichst seinen Zylinder im Betrieb nicht anfassen sollten, um uns nicht die Finger zu verbrennen! Diese Alltagserfahrung lehrt uns, dass Luft durch Verdichten erwärmt wird. Auch den umgekehrten Fall kann man gut nachweisen, wenn man am gefüllten Kompressorbehälter das Ventil öffnet: Das Ventil wird durch die ausströmende Luft kalt und kälter, die Feuchtigkeit der Umgebungsluft schlägt sich daran nieder und bei genügend großem Luftvorrat kann es bis zur Reifbildung kommen. Letztlich kann man durch solche Spielchen Luft sogar so weit abkühlen, dass sie flüssig wird! Wer's nicht glaubt, soll sich im Deutschen Museum in München davon überzeugen! |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ausdehnung heißt AbkühlungUnser mitgeführtes Luftpaket wird also nicht nur größer, sondern durch dieses Ausdehnen auch kälter. Die Abkühlung kommt dabei nur vom Ausdehnungsprozess durch die Druckabnahme und nicht von der ja auch kälter werdenden Umgebung; schließlich haben wir es ja zu 100% wärmeisoliert! Auch diese Abkühlung lässt sich berechnen:
Alle diejenigen, die's genauer wissen wollen, finden die Herleitung dieser Formel unter dem Stichwort Isentropische Zustandsänderung in jeder besseren physikalischen Formelsammlung (beispielsweise im Kuchling: Taschebuch der Physik). Bis auf den Exponent sieht die Formel ja recht harmlos aus: Die Temperaturverhältnisse hängen mit den Druckverhältnissen zusammen. Jedoch müssen wir auch die Wärmekapazität des beteiligten Gases, also der Luft berücksichtigen. Die Wärmekapazität gibt an, wie stark die Temperatur eines Stoffes zunimmt, wenn man ihm Energie zuführt. Bei einer bestimmten Menge eines Stoffes mit großer Wärmekapazität braucht man für die selbe Temperaturzunahme mehr Energie als für dieselbe Menge eines Stoffs mit kleiner Wärmekapazität. Um beispielsweise 1 kg Holz um 10 °C zu erwärmen, benötigt man etwa 25 kJ. Ein kg Eisen benötigt für dieselbe Temperaturzunahme nur 4,5 kJ. Um einen Liter Wasser um 10 °C zu erwärmen, benötigen wir fast 42 kJ. Die spezifische Wärmekapazität eines Stoffes gibt ganz bildlich gesprochen seine Fähigkeit an, Energie aufzunehmen, ohne dies gleich durch starke Temperaturzunahme zu "verraten". Auch Gase besitzen eine solche spezifische Wärmekapazität und sogar nicht nur eine, sondern deren zwei! Führt man einem Gas Energie zu, so daß sich seine Temperatur erhöht, wird es sich, so es kann, ausdehnen, also bei gleichem Druck sein Volumen vergrößern. Sperrt man das sich erwärmende Gas aber in ein festes Volumen ein, dann reagiert es mit einer Druckerhöhung. Da Lustige daran ist: Je nach dem hat das Gas eine andere spezifische Wärmekapazität: Im ersten Fall, also bei sich vergrößerndem Volumen und konstantem Druck hat Luft eine spezifische Wärmekapazität von cp = 1,005 Bei adiabatischen Zustandsänderungen von Gasen spielt der Quotient aus beiden spezifischen Wärmekapazitäten eine Rolle, er beträgt 1,402 und wird in der Formel durch das kleine griechische Kappa dargestellt. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Temperaturabnahme des hochtransportierten LuftpaketsDamit haben wir schon alle benötigten Formeln zusammen, um die Temperaturabnahme unseres transportierten und gut isolierten Luftpakets zu berechnen: Mit der internationalen Höhenformel bestimmen wir die Druckabnahme mit der Höhe und über die zweite Formel schließen wir daraus auf die Temperaturabnahme. Diese Berechnungen stellen wir natürlich nicht von Hand an, wofür gibt es denn Tabellenkalkulationssysteme?
Benutzereingaben erfolgen nur in die drei gelb hinterlegten Felder, alle anderen Werte werden davon abhängig berechnet. Im obigen Beispiel sind die ICAO-Standardwerte eingetragen und man sieht deutlich, wie mit zunehmender Höhe der Druck und die Temperatur unseres hochtransportierten Luftpakets abnehmen. Erstaunlich ist, dass die Temperaturabnahme fast linear erfolgt, obwohl die verwendeten Formeln ganz "krumme" Exponenten beinhalten. Die Temperaturabnahme des transportierten Luftpakets beträgt knapp 1 °C pro 100 m Höhenunterschied und genau dies ist der trockadadiabatische Hebungsgradient! |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Der trockenadiabatische HebungsgradientEr wird "Hebungs"-Gradient genannt, weil wir das Luftpaket ja hochtransportieren und damit mechanisch anheben. Es ist ein adiabatischer Hebungsgradient, weil wir dank unserer optimalen Verpackung jeglichen Energie- und damit Wärmeaustausch mit der Umgebung verhindern. Und trocken ist er schließlich, weil wir unten in Garmisch ein vollständig trockenes Luftpaket ohne bereits kondensierenden Wasserdampf eingepackt haben. Welche Temperatur hat denn unser Luftpaket, wenn wir endlich auf dem Gipfel angekommen sind? In der folgenden Tabelle sind als Ausgangswerte die schon weiter oben angenommenen Daten für Garmisch-Partenkirchen eingetragen, nämlich 20°C in 800 m Höhe. Mit diesen Werten haben wir quasi unsere Luft eingepackt.
Auf dem Gipfel in 3000 m Höhe kommt es mit –1,64 °C an, es ist also fast 7 °C kälter als die Umgebungsluft am Schneefernerhaus. Aufgrund des Schichtungsgradienten hatten wir ja eine Umgebungstemperatur von etwa + 5 °C bestimmt. Die zugehörige EXCEL-Tabelle heißt adiabate.xlsx, sie kann hier für eigene Versuche heruntergeladen werden. Damit kann jeder selbst nach Belieben Ausgangswerte variieren und die Auswirkungen beobachten. Verblüffend ist, dass sich die Temperaturwerte und damit die Temperaturdifferenzen nicht ändern, wenn man das QNH, also den Druck in Meereshöhe verändert. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Feuchte LuftWas aber wäre gewesen, wenn wir feuchte Luft eingepackt hätten? Wenn es einen trockenadiabatischen Hebungsgradienten gibt, ist ein feuchtadiabatischer sicher nicht weit! Um selbigen zu erklären, müssen wir jedoch wieder ein wenig ausholen: Wasser ist ein ganz wichtiger Faktor des Wettergeschehens. Man kann ohne Übertreibung sagen, dass es ohne Wasser gar kein Wetter gäbe! Wasser tritt in allen drei Aggregatzuständen in der Atmosphäre auf: flüssig, gasförmig und fest. Dabei ist es ein alter Irrglaube, dass Wolken aus Wasserdampf bestehen, Wasserdampf ist nämlich unsichtbar! Wer damit Probleme hat, sehe mal ganz genau hin, wenn Mutter in der Küche den Sicomatic abdampft. Direkt an der Austrittsstelle und noch 2 - 3 cm danach sieht man gar nichts! Erst in größerer Entfernung vom Topf beginnen sich Nebelschwaden zu formieren. Jetzt ist der vormals heiße Wasserdampf aufgrund der relativ kühlen Umgebung bereits wieder in flüssiges Wasser kondensiert. Was man sieht, sind also bereits winzige Wassertröpfchen! Luft kann also sehr wohl Wasserdampf (also gasförmiges Wasser) enthalten, ohne dass wir dies sehen. Wenn wir etwas sehen, handelt es sich also immer um flüssiges Wasser. Wolken bestehen demnach aus flüssigem oder auch schon gefrorenem Wasser in winziger Tropfen- oder Kristallform. Für unsere weiteren Überlegungen sind insbesondere die Übergänge zwischen den drei Zuständen von Interesse. Deshalb betrachten wir mal was passiert, wenn Wasser verdampft. Um diesen Phänomenen auf die Spur zu kommen, brauchen wir neben einem Topf Wasser auf dem Herd nur noch einen Thermometer. Jeder Mensch weiß, dass die Temperatur des Wassers steigt, wenn wir die Herdplatte einschalten. Wir führen Energie zu, also steigt, entsprechend der spezifischen Wärmekapazität des erwärmten Stoffes dessen Temperatur. Weiter oben haben wir schon mal erwähnt, daß 1 kg Wasser etwa 42 kJ Energie für eine Temperaturzunahme um 10 °C benötigt. In früheren Zeiten, als alles noch viel besser war, haben die schlanken Damen beim Essen Kalorien gezählt und die Physiker mit eben solchen gerechnet (den Kalorien, nicht mit den Damen!). Das waren noch Zeiten! Die alte Energieeinheit "Kalorie" war nämlich quasi auf das Wasser "geeicht" und lieferte viel schönere Werte als das neumodische Joule. Wir fallen deshalb kurzfristig wieder in diese alten schönen Zeiten zurück, die eben angestellte Rechnung lautet nun: Um 1 kg Wasser um 10 °C zu erwärmen, benötigt man die Energiemenge von 10 Kilokalorien. Oder, was genau das selbe ist: 1 Kilokalorie für 1 °C pro kg. Stellen wir unseren Topf mit einem Kilogramm 20 °C kaltem Wasser auf den Herd, so brauchen wir 80 Kilokalorien, um diese Menge auf 100 °C zu erwärmen. Diese Temperaturzunahme stellen wir problemlos mit unserem Thermometer fest: Es steigt langsam aber stetig an. Wie jeder Mensch glaubt, siedet Wasser bei dieser Temperatur, der Verdampfungsprozess ist damit in vollem Gange. Es brodelt und dampft, die Herdplatte feuert nach wie vor auf höchstem Niveau, nur unser Thermometer macht keinen Ruck mehr. Es bleibt wie angewurzelt auf 100 °C stehen! |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Energieträger Wasserdampf
Spätestens jetzt sollten wir ins Grübeln kommen: Wohin gehen denn all die schönen und teuren Kalorien, welche die Herdplatte nach wie vor liefert? Für eine Temperaturerhöhung des Wassers kommen sie nicht mehr in Frage, wie das Thermometer beweist. Diese Energie kann auch nicht verschwinden; das verhindert der Satz von der Erhaltung der Energie. Der einzige Prozess, der jetzt noch abläuft ist der Verdampfungsprozess und genau dafür werden all die Kalorien benötigt. Um aus flüssigem Wasser Dampf gleicher Temperatur zu machen, braucht man wahnsinnig viel Energie. Wollen wir den ganzen Liter Wasser verdampfen, so müssen wir dafür fast 600 Kilokalorien aufwenden. Im Vergleich dazu nehmen sich die oben errechneten 80 Kilokalorien zum Erwärmen geradezu lächerlich aus! Diese Energie steckt nun im Dampf. Lassen wir ihn wieder kondensieren, so wird genau diese Energiemenge als Kondensationswärme wieder frei. Wasserdampf ist also erstens ein ordentlicher Energieträger. Zweitens wirkt er ungemein ausgleichend, weil er in Zeiten des Überschusses sehr viel Energie aufnehmen und in Mangelzeiten wieder abgeben kann. Ohne Wasserdampf, bzw. ohne seine Fähigkeit zur Energiespeicherung hätten wir viel krassere Temperaturunterschiede auf der Erde. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Wasserdampf in der LuftDas im Topf verdampfende oder auf der Erdoberfläche verdunstende Wasser steigt hoch in die Atmosphäre und befindet sich als unsichtbares Wassergas in der Luft. Es wird in kühlen Nächten sichtbar, wenn es sich in flüssiger Form als Tau auf dem Gras und den Autoscheiben niederschlägt. Wer nicht in die Kälte raus will, bestelle sich in seiner Kneipe ein kühles Bier und beobachte dann am Glas genau das selbe Phänomen. Wir lernen daraus, dass die Luft den enthaltenen Wasserdampf bei niedrigen Temperaturen auch wieder abgibt. Ganz bildhaft können wir uns Luft als Schwamm vorstellen, welcher Wasser aufnehmen und speichern, aber auch wieder abtropfen lassen kann. Dabei hängt die Speicherfähigkeit unseres Luftschwamms einzig und allein von seiner Temperatur ab: Je höher die Lufttemperatur, um so mehr Wasserdampf kann sie aufnehmen. Für diese "Speicherfähigkeit" der Luft gibt es eine grobe, aber dennoch ausreichende Faustformel: Ein Kubikmeter Luft kann maximal so viel Wasserdampf in Gramm aufnehmen, wie es dessen Temperatur in °C entspricht. Kurz: 1 Kubikmeter Luft von 10°C kann maximal 10 g Wasserdampf aufnehmen; wollen wir 20 g Wasserdampf unterbringen muss die Luft mindestens 20 °C warm sein. Davon wird weiter unten noch ausführlich die Rede sein. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Zurück nach GarmischPacken wir in Garmisch wieder einen Kubikmeter Luft mit 20° C in unsere phänomenale Isolierhülle. Diesmal nehmen wir aber welche, die genau 10 g Wasserdampf enthält. Wie wir leicht rechnen (1 °C / 100 m) oder in der obigen Tabelle nachschauen können, müssen wir genau 1000 m aufsteigen, bis sich unser Luftpaket auf 10 °C abgekühlt hat. Obwohl jetzt Dampf in der Luft enthalten ist, können wir anfangs problemlos so tun, als sei sie völlig trocken. Solange nämlich das enthaltene Wasser ausschließlich als unsichtbares Gas enthalten ist, hat dies überhaupt keine Auswirkungen auf unsere zuvor angestellten Überlegungen und Berechnungen. Steigen wir jedoch höher und kühlt sich die Luft weiter ab, so ist der enthaltene Wasserdampf nicht mehr länger zu halten, da für 10 g Dampf mindestens 10 °C Lufttemperatur nötig sind. Jede weitere Abkühlung führt also zur Kondensation des überschüssigen Dampfes. Wenn unsere Super-Hülle auch noch durchsichtig ist, sehen wir, dass wir nun eine kleine Wolke den Berg hoch tragen. Bei dieser Kondensation wird die im Dampf gespeicherte Kondensationswärme wieder frei. Dies führt dazu, dass sich das Luftpaket auf dem weiteren Weg nach oben nun nicht mehr um 1 °C pro 100 m Höhenunterschied abkühlt. Die Temperaturabnahme ist aufgrund der aus dem kondensierenden Wasserdampf stammenden Energie geringer und beträgt je nach Wasserdampfgehalt und Ausgangstemperatur zwischen 0,3 und 0,9 °C; im Mittel rechnen wir mit 0,6 °C. Dies ist der feuchtadiabatische Hebungsgradient. Um das Beispiel weiter zu "gehen": Steigen wir die restlichen 1200 m bis zum Gipfel hoch und kühlt sich die transportierte Luft nur noch mit 0,6 °C pro 100 m ab, so ist unser Luftpaket oben mit +2,8 °C zwar immer noch kälter als die Umgebungsluft aber doch deutlich wärmer als das zuvor trocken transportierte Paket. Die besprochenen Gradienten geben immer die Größe einer Temperaturabnahme mit zunehmender Höhe an. Dabei muss zuerst unterschieden werden, ob wir die Temperaturabnahme einer ruhenden Luftschicht messen, wo es in größerer Höhe einfach deshalb kälter wird, weil wir uns immer weiter von der "Heizplatte" Erdboden entfernen. Im anderen Fall heben wir Luft mechanisch hoch. Dabei wir die Luft kälter, weil sie sich ausdehnt. Unterschieden werden muss hier noch, ob die gehoben Luft trocken (also ohne sichtbare Kondensation) ist oder feucht.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Und die Realität?Bei unseren Überlegungen haben wir eine "phänomenale Verpackung" verwendet, welche das Luftpaket ideal wärmeisoliert, sonst aber nicht einengt oder behindert. So was gibt es natürlich in der Realität nicht, brauchen wir aber auch gar nicht: Luft selbst ist nämlich ein sehr schlechter Wärmeleiter und damit ein gutes Wärmeisolationsmaterial. Nicht umsonst hüllen wir uns an kalten Tagen in Daunenanoraks; die enthaltenen Federn dienen nur dazu, ein möglichst dickes Luftpolster um uns herum zu erzeugen. Außerdem fährt man kaum in der Seilbahn gut isolierte Luftpakete spazieren. Das braucht es aber genau so wenig, denn mehr oder weniger große Luftpakete steigen ganz von selbst in die Höhe oder sinken aus der Höhe wieder hinab zum Erdboden: Eine am Erdboden vom warmen Untergrund erhitzte Luftschicht spielt einfach Heißluftballon und steigt in die Höhe. Darauf hat der Segel-, Drachen- oder Gleitschirmflieger schon gewartet und er lässt sich in dieser Thermikblase mit nach oben tragen. Wie weit es nach oben geht, kann man relativ einfach aus der Kenntnis einiger Temperaturwerte und der hier erklärten Gradienten bestimmen. Doch das ist eine andere Geschichte und bevor wir uns dieser zuwenden, müssen wir noch ein paar Worte über die Feuchtigkeit in der Luft verlieren. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
LuftfeuchtigkeitWie kommt Feuchtigkeit in die Luft? Nun, wir haben weiter oben schon kurz erwähnt, dass Wasser bei 100°C kocht und in seinen gasförmigen Zustand übergeht. Nun haben wir einzelne Wassermoleküle, die sich zwischen den Stickstoff- und Sauerstoffmolekülen der Luft tummeln. Um Wasserdampf im größeren Stil in die Luft zu bekommen, braucht es allerdings keine Kochtöpfe mit kochendem Wasser. Wasser verdunstet von ganz allein. Dies erkennt man problemlos daran, dass die nach einem Regen nasse Straße samt ihrer Pfützen im Lauf der Zeit abtrocknet: Das flüssige Wasser ist in seinen dampfförmigen Zustand übergetreten und im wahrsten Sienne des Wortes in der Luft verschwunden. Für die Erklärung dieses Phänomens müssen wir uns kurz mit der physikalischen Größe "Temperatur" beschäftigen. Temperatur ist letztlich die Bewegungsenergie der Teilchen, aus denen ein Stoff besteht. In einem Gas sausen die Atome oder Moleküle frei umher und je höher die Bewegungsgeschwindigkeit der Teilchen ist, umso heißer ist das Gas. Dabei ist es keinesfalls so, dass alle Teilchen genau dieselbe Geschwindigkeit haben. Es gibt vielmehr schnellere und langsamere Teilchen und die Durchschnittsgeschwindigeit aller Teilchen im Gas ergibt die Temperatur. In einer Flüssigkeit, beispielsweise in Wasser, sind die Wassermoleküle auch frei beweglich und diese bewegen sich – entsprechend der Temperatur des Wassers – mehr oder weniger schnell. Auch hier gibt es wieder schnellere und langsamere Wassermoleküle. Man kann sich nun ganz bildhaft vorstellen, dass es die ganz schnellen Teilchen schaffen, das flüssige Wasser zu verlassen und dann als einzelne Wassermoleküle durch die darüberliegende Luft schwirren. Sie sind somit aus dem flüssigen in den gasförmigen Zustand übergetreten. Wenn die schnelllsten Teilchen aus dem Wasser "fliegen", dann sinkt notgedrungen die Durchschnittsgeschwindigkeit der zurückbleibenden Moleküle. Dies bedeutet, dass die Temperatur des Wassers sinkt. Man nennt dies die "Verdunstungskälte" und genau nach diesem Prinzip funktioniert die Aufrechterhalung unserer Körpertemperatur bei Hitze durch Schwitzen! Für die Verdunstung auf der Straße spielt dies keine große Rolle, da ja meist die Sonne scheint und diesen Energieverlust im Wasser wieder ausgleicht. Es lässt sich auch unschwer beobachten, dass der Verdunstungsprozess in der Wärme des Sonnenscheins besser funktioniert als im kühlen Schatten. Um den Verdunstungsprozess etwas genauer untersuchen zu können, schütten wir eine Wasserpfütze in einen größeren Behälter mit Luft und beobachten, was da geschieht. Genau wie eben erwähnt, werden die schnelleren Wassermoleküle die Flüssigkeit verlassen und als Gas zwischen der Luft hin- und hersausen. Dabei stoßen sie mit anderen Molekülen und mit der Behälterwand zusammen und üben auf diese eine Kraft aus. Wenn eine Kraft auf eine Fläche wirkt, dann sprechen wir vom Druck, in diesem Fall konkret vom Dampfdruck. Es leuchtet unmittelbar ein, dass dieser Dampfdruck umso größer ist, je mehr Wassermoleküle durch die Luft schwirren. Der Dampfdruck wächst somit mit der Menge des Wasserdampfs, welcher sich in der Luft befindet.
Irgendwann ist aber Schluss mit der Menge des Wasserdampfs, der sich in der Luft befinden kann. Man sagt, dass in diesem Fall der Sättigungsdampfdruck erreicht ist. In dem Luftvolumen ist dann die größtmögliche Wasserdampfmenge enthalten. Man ist nun geneigt zu glauben, dass diese größte Wasserdampfmenge von der Menge der Luftteilchen und damit vom Luftdruck abhängig ist, weil halt irgendwann der Platz für alle knapp wird. Dem ist jedoch nicht so! Die Menge des Wasserdampfs, den die Luft über der Pfütze aufnehmen kann, ist einzig und allein von der Lufttemperatur abhängig. Klingt komisch – ist aber einfach so. In phyikalischen Büchern kann man Tabellen finden, in denen der Sättigungsdampfdruck in Abhängigkeit von der Lufttemperatur dargestellt ist:
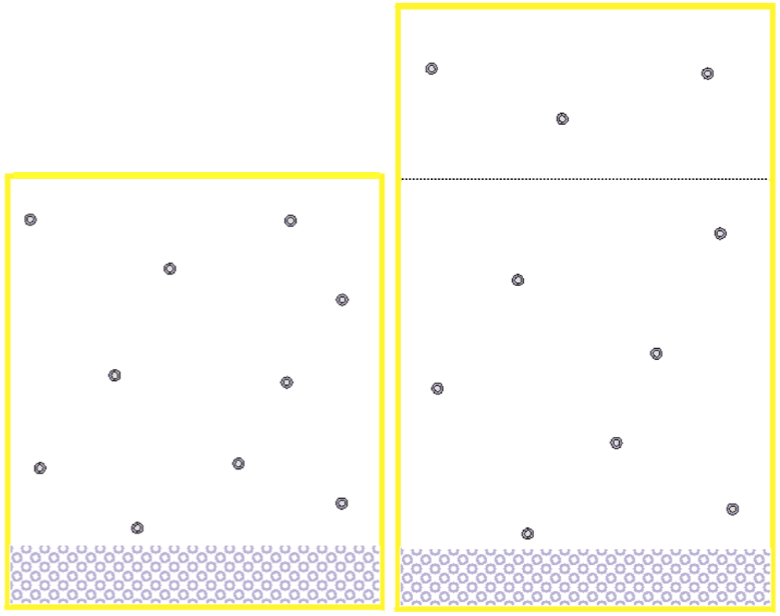
Danach kann ein Kubikmeter Luft genau so viel Gramm Wasserdampf aufnehmen, wie es seiner Temperatur in Celsius entspricht. Diese verinfachte Zurodnung ist für unsere überschlägigen Berechnungen völlig ausreichend. Enthält ein Kubikmeter Luft die entsprechend seiner Temperatur mögliche, maximale Wasserdampfmenge, so sprechen wir hierbei von der maximalen Feuchtigkeit. DIe maximale Feuchtigkeit gibt somit ungekehrt an, wie viel Wasserdampf in g/m3 ein Kubikmeter Luft einer bestimmten Temperatur tragen kann. In aller Regel ist aber weniger Wasserdampf als die maximal mögliche Menge enthalten. Die tatsächlich enthaltene Menge an Wasserdampf nennt man die absolute Feuchte der Luft. Nun ist die alleinige Kenntnis der absoluten Feuchte nicht besonders hilfreich, weil uns der Bezug fehlt: Was sagt es uns, wenn wir wissen, dass die Luft auf dem Flugplatz 17g/m3 Wasser enthält? Diese Aussage wird erst hilfreich, wenn wir als erfahren, wie viel denn maximal drin sein könnten! Man bildet deshalb den Quotienten aus absoluter Feuchte geteilt durch maximale Feuchte und drückt diesen in Prozent aus. Daraus erhalten wir die relative Feuchte und die Angabe, dass die relative Feuchte beispielsweise 87% beträgt, macht uns wesentlich schlauer: Wissen wir doch, dass die Luft schon zum größten Teil mit Wasserdampf gesättigt ist. Hierzu gleich noch ein paar Rechenbeispiele: Unser Thermometer zeige eine Lufttemperatur von 20°C und unser Hygrometer eine relative Feuchte von 80%. In Luft von 20°C könnten – nach unserer obigen Faustformel – maximal 20 g/m3 Wasserdampf enthalten sein. Enthalten sind aber nur 80% und damit 16 g/m3, dies ist die absolute Feuchte. Was passiert, wenn am Abend die Lufttemperatur sinkt und wir nur noch 18°C messen? Die absolute Feuchte hat sich dabei nicht geändert. Jetzt haben wir eine maximale Feuchte von 18g/m3 bei einer absoluten Feuchte von nach wie vor 16 g/m3, woraus wir problemlos eine relative Feuchte von etwa 89% errechnen. Temperaturänderungen – welche in der Atmosphäre relativ leicht auftreten können – führen somit bei gleichbleibender Feuchte (und die Feuchte einer Luftmasse ist deutlich konstanter) zu einer Änderung der relativen Feuchte. Sinkt die Temperatur, so steigt die relative Feuchte! Jetzt fragen wir, wie weit kann denn die Temperatur der Beispielluft abkühlen, bis wir die maximale Feuchte erreichen? Die Antwort ist leicht, wir haben ja eben errechnet, dass die absolute Feuchte 16 g/m3 beträgt, damit kann die Luft auf 16°C abgekühlt werden, bis sie 100% relativer Feuchte erreicht und gesättigt ist. Diese Temperatur, bis zu welcher man ein Luftpaket (bei gleichbleibender absoluter Feuchtigkeit) abkühlen muss, um 100% relative Luftfeuchtigkeit zu erreichen, nennt man den Taupunkt. Die Namensgebung kommt daher, weil sich im Moment des Erreichens des Taupunkts die als Dampf enthaltene Feuchtigkeit in der Luft nicht mehr halten kann, sondern auskondensiert und sich beispielsweise als Tau auf dem Gras niederschlägt. Für uns Flieger ist nun gerade der Taupunkt eine wichtige, weil sehr anschauliche Bezugsgröße. Der Feuchtegehalt einer Luftmasse wird daher in der Flugmeteorologie durch die Paarung Lufttemperatur und Taupunkt ausgedrückt: Wenn wir hören, dass die Lufttemperatur 30°C beträgt und der Taupunkt bei 12°C liegt, dann müssen wir keine Sichtbehinderungen in Form von Nebel befürchten, der ja immer im Zusammenhang mit Kondensaton auftritt. Wenn die Temperatur jedoch mit 15°C angegeben ist und der Taupunkt 13°C beträgt, dann ist höchste Vorsicht geboten: Bei einer Abkühlung von nur 2°C wird Nebelbildung einsetzen! Der Taupunkt ist also diejenige Temperatur, bei der eine gegebene Luftmasse zu kondensieren beginnt. Die enthaltene Feuchtigkeit wird jetzt als Nebel oder Wolke sichtbar. Damit kommen wir wieder zu unserer Ausgangsproblemtik zurück: Wenn ein Luftpaket vom Boden aus aufsteigt, so enthält es immer eine bestimmte Menge an Feuchtigkeit. Aufgrund dessen absoluter Feuchte kennen wir dessen Taupunkt und damit können wir in der Folge leicht berechnen, in welcher Höhe durch die trockenadiabatische Abkühlung dieser Taupunkt erreicht wird und Wolkenbildung einsetzt. Wenn wir für diese Rechnung beispielhaft die eben erwähnte Luftmasse mit 20°C und einem Taupunkt von 16°C zugrundelegen und wenn wir wissen, dass sich das trockenadiabatisch aufsteigende Luftpaket um 1°C/100 m abkühlt, dann lässt sich daraus leicht errechnen, dass sich diese Luft in 400 m Höhe auf 16°C abgekühlt haben wird. So weit, so richtig. Allerdings wird nun die Kondensation trotzdem nicht in 400 m einsetzen! Um diesen vermeintlichen Widerspruch auflösen zu können, muss man wissen, dass der Taupunkt, welchen das Luftpaket am Boden besitzt, mit zunehmender Höhe nicht gleich bleibt, sondern sich ändert! Zum Verständnis dieses Phänomens bemühen wir wieder unsere Modellvorstellung von einem angeschlossenen Luftvolumen von einem Kubilmeter, in welchem sich unten eine Wasserpfütze befindet. Um die Angelegenheit überschaubar zu machen, legen wir fest, dass aus der Pfütze genau zehn Wassermoleküle in das darüberliegende Luftvolumen von einem Kubikmeter verdunsten sollen, um die maximale Feuchte zu erreichen. Dies ist im linken Bild dargestellt. Wenn wir nun dieses Luftpaket hochsteigen lassen, wird es sich – da es in Gebiete niedrigeren Luftdrucks gerät – ausdehnen, also sein Volumen vergrößern. Die zuvor verdunsteten zehn Wasserdampfmoleküle verteilen sich jetzt also auf ein größeres Volumen. Dies bedeutet, dass in dem ursprünglichen Kubikmeter (in unserem Beispiel) nur noch sieben Wasserdampfmoleküle vorhanden sind (rechtes Bild). Diese sieben Wasserdampfmoleküle sind nun aber weniger, als die maximal möglichen zehn Dampfmoleküle. Es gibt nun zwei Möglichkeiten, die maximale Feuchte wieder herzustellen: Entweder verdunsten drei zusätzliche Wasserdampfmoleküle aus dem Wasser in die Luft oder aber wir können die Temperatur im Luftpaket senken, bis sieben Moleküle das Maximum darstellen. Weil wir unser Luftpaket aber nach oben wegbewegt haben, bleibt die Pfütze am Boden zurück und steht nicht mehr als Quelle für die drei zu verdunstenden Wassermoleküle zur Verfügung. Den ersten Fall können wir daher ausschließen. Bleibt nur noch der zweite Fall mit der Absenkung der Temperatur. Natürlich ist die Temperatur im Paket schon aufgrund des Hochhebens und der Volumenausdehnung etwas gesunken. Aber eben nicht so stark, dass dabei die maximale Feuchte erhalten geblieben ist, wir können also die Temperatur darüber hinaus noch etwas weiter absenken, um die maximale Feuchte wieder zu erreichen. Dies bedeutet, dass sich der Taupunkt in einem aufsteigenden Luftpaket verringert und diese Taupunktsabnahme mit der Höhe beträgt genau 0,2°C/100 m. Unsere Berechnung für die Höhe der Wolkenbasis müssen wir somit etwas modifizieren: Die Temperatur im aufsteigenden Puftpaket nimmt um 1°C/100 m ab, der Taupunkt nimmt aber auch ab und zwar um 0,2°C/100 m. Deshalb nähert sich die Temperatur des aufsteigenden Pakets dem Taupunkt eben nicht um 1°C/100 m, sondern nur um 0,8°C/100 m an. Unsere Rechnung lautet daher
und wir erhalten eine Basishöhe von 500 m. Um Basishöhen auszurechnen, muss man also lediglich die Taupunktsdifferenz, den sogenannten Spread, mit dem Faktor 125 multiplizieren. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
MessballoneDass der Schichtungsgradient nach ICAO nur ein statistischer Mittelwert ist und mit dem tatsächlichen Temperaturverlauf in der Atmosphäre recht wenig zu tun hat, wurde bereits erwähnt. Dieser tatsächliche Temperaturverlauf der Luftschicht ist allerdings für die Wettervorhersage dermaßen entscheidend, dass die Meteorologen auf der ganzen Welt einen beträchtlichen Aufwand betreiben, eben diesen Temperaturverlauf täglich mehrfach zu messen. Hierfür lässt man Ballone in die Höhe steigen, an denen sogenannte Radiosonden mit Sensoren zur Aufnahme der meteorologischen Parameter wie Temperatur, Druck und Feuchte angebracht sind. Außerdem ist ein kleiner Sender dabei, welcher die aufgenommenen Messwerte zur Erde funkt. Schließlich war früher am Ballon noch ein Radarreflektor angebracht, um den Ballon verfolgen zu können. Durch die Verfolgung mittels Radar ließen sich die Höhenwinde in der Atmosphäre bestimmen. Heute nimmt der Ballon einen GPS-Empfänger mit nach oben, welcher fortlaufend die aktuelle Position ermittelt. Durch den Aufstieg dehnt sich der Ballon immer weiter aus, bis er schließlich und meist inmitten der Stratosphäre platzt. Die Radiosonde schwebt dann an einem Fallschirm zur Erde zurück. Genaueres zur Technik der Wetterballone und Radiosonden findet man im Internet: https://de.wikipedia.org/wiki/Wetterballon https://de.wikipedia.org/wiki/Radiosonde Aufgrund der technischen Fortschritte ist es heute für Jedermann möglich, einen "Wetter"ballon in die Stratosphäre zu senden. Es gibt sogar eine Internetseite, welche Anleitungen für solche privaten Missionen bereithält: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Der TempDer Meteorologe erhält aus den von der Radiosonde zur Erde gefunkten Daten ein umfassendes Bild über den Zustand der Atmosphäre: Über den uns hier primär interessierenden Temperaturverlauf erhält er weitere Informationen über den Feuchteverlauf, den Luftdruck und die Höhenwinde in der Atmosphäre. Bereits aus dem Temperaturverlauf in der Atmosphäre, dem sogenannten Temp und dem Taupunkt am Boden, lassen sich in idealisierter Form bereits sehr aufschlussreiche Aussagen zum Wetter ableiten. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Auswertung eines Temps |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
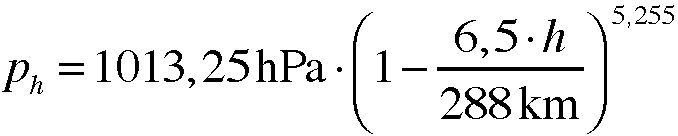
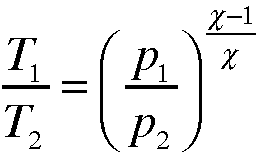
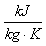 . Um 1 kg Luft um 10°C zu erwärmen braucht es in diesem Fall also etwa 10 kJ. Lässt man beim Erwärmen das Volumen konstant, so dass sich der Druck erhöht, beträgt die spezifische Wärmekapazität von Luft nur noch cv = 0,717
. Um 1 kg Luft um 10°C zu erwärmen braucht es in diesem Fall also etwa 10 kJ. Lässt man beim Erwärmen das Volumen konstant, so dass sich der Druck erhöht, beträgt die spezifische Wärmekapazität von Luft nur noch cv = 0,717